Решение
Восстановим удобочитаемую структуру программы.
(1) struct k{ int m[4]; };
(2) k m(k m1, k m2) {
(3) return k{m1.m[0]*m2.m[0]+m2.m[2]*m1.m[1], m2.m[1]*m1.m[0]+m1.m[1]*m2.m[3],
(4) m2.m[0]*m1.m[2]+m2.m[2]*m1.m[3], m2.m[1]*m1.m[2]+m1.m[3]*m2.m[3]};}
(5) }
(6) int g(int n) {
(7) k p={0,1,1,1};
(8) k r={1,0,0,1};
(9) while(n) {
(10) if(n&1)
(11) r=m(r, p);
(12) p=m(p,p);
(13) n>>=1;
(14) }
(15) return r.m[ 2 ];
(16)}
Можно убедиться, что при n=1 функция возвращает 1, при n=2 – 1, при n = 3 – 2, при n = 4 – 3, при n = 5 – 5. Сделаем предположение, что функция генерирует последовательность натуральных чисел каждое из которых, начиная с третьего члена является суммой двух предыдущих чисел.
Используем для обозначения функции m(m1,m2) обозначение m1*m2.
Рассмотрим последовательность действий, которые выполняет функция при n = 1.В этом случае легко заметить, что r = r*p, при этом заполнение r есть {0,1,1,1}. Легко убедиться, что в этом случае функция mвернет значение равное p = {0,1,1,1}. Более того, если один из аргументов функции mравен {0,1,1,1}, то ее значение равно второму аргументу. На второй итерации условие 9 не будет выполнено и будет возвращено значение 1.
Рассмотрим два случая: n – четно и n – нечетно.
Обозначим p0 = {0,1,1,1}. Легко убедиться, что на итерации tцикла значение переменной pбудет равно pt = (p02)t = p0 * … * p0.
Если n = 2s – четно, то условие в строке 10 не выполнено и p1=p0*p0 и значение r не поменяется. На следующей итерации nбудет равно s. Если s четно, тогда на следующей итерации p2=p1*p1=p0*p0*p0*p0 и значение rснова остается прежним т.д.
Если n = 2s+1 – нечетно, то условие в строке 10 выполнено и r = r*p, а p1 = p*p.
Таким образом, после завершения цикла 9-14 r будет содержать значение pt = p0n. Данный способ расчета значения nназывается методом бинарного возведения в степень.
Рассмотрим функцию m. Легко заметить, что данная функция выполняет умножение матриц m1 и m2.
Покажем, что функция g генерирует последовательность натуральных чисел каждое из которых, начиная с третьего члена является суммой двух предыдущих чисел.
Пусть 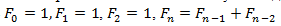
Легко убедиться, что

Заметим, что
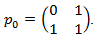 .
.
Откуда,

Заметим, что так как
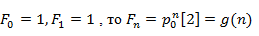
Таким образом, мы показали, что функция g генерирует последовательность натуральных чисел каждое из которых, начиная с третьего члена является суммой двух предыдущих чисел.