Решение
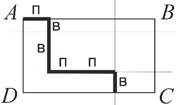
На рисунке изображен исходный прямоугольник ABCD, разбитый на маленькие прямоугольники. Предположим, что путник, находящийся сейчас в вершине A, хочет добраться или до стороны BC, или до стороны CD (до какой получится раньше – путнику все равно). При этом ему разрешается двигаться:
- только по сторонам маленьких прямоугольников;
- только вниз (в) или вправо (п);
- только по сторонам, имеющим четную длину (у каждого прямоугольника хоть одна сторона четная, поэтому путнику всегда будет куда пойти).
На рисунке путник добрался до стороны CD по траектории пввппв (за один ход путник смещается вниз или вправо на расстояние, не менее 1, а значит, рано или поздно, цели своего путешествия он достигнет). Ясно, что длина стороны AD равна сумме длин всех отрезков в его траектории. Каждый такой отрезок четен, а значит, и длина стороны AD четна. Аналогично доказывается четность длины стороны AB в случае, если путник прежде достиг стороны BC. Утверждение доказано.