Решение
Перепишем равенство в виде:
^2 + \left( {\frac{y}{z}} \right)^2 = 10,
})
где
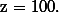
Обозначив
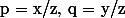
, получим уравнение
Задача сведена, таким образом, к поиску точек с положительными рациональными координатами (со знаменателем 100) на окружности радиуса
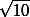
с центром в начале координат. Уравнению (1) удовлетворяют, например, числа

Остальные рациональные точки будем искать следующим образом: через точку с координатами

будем проводить всевозможные прямые
а коэффициент k подбирать так, чтобы точка пересечения прямой (2) и окружности (1) (отличная от

) имела рациональные координаты. Подставив (2) в (1), получим:
 + 3} \right)^2 + q^2 = 10\, \Leftrightarrow \,k^2 \left( {q - 1} \right)^2 + 6k\left( {q - 1} \right) + q^2 - 1 = 0\, \Leftrightarrow
})
 + 6k + q + 1 = 0 \Leftrightarrow \,q = \frac{{k^2 - 6k - 1}}{{1 + k^2 }}.})
Подставляя полученное выражение для q в (2), найдем

Поскольку
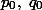
рациональны, а в точке пересечения рациональными должны быть еще и
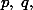
то, как следует из (2), коэффициент k также рационален. Полагая

выражения для p и q перепишем в виде
 - 2mn}}{{n^2 + m^2 }},\quad \quad q = \frac{{m^2 - 6mn - n^2 }}{{n^2 + m^2 }}.
})
Таким образом, искомые числа равны
 - 2mn, \quad y = m^2 - 6mn - n^2 {\rm{,}}
})
где

Последнее уравнение решается перебором:
,\,\,\left( {\left| m \right| = 0,\,\left| n \right| = 10} \right),\,\,\left( {\left| m \right| = 8,\,\left| n \right| = 6} \right),\,\,\left( {\left| m \right| = 6,\,\left| n \right| = 8} \right).})
Для найденных m, n (а также с учетом отмеченного ранее решения

) получаем следующие пары натуральных чисел (x, y):
(12, 316), (100, 300), (180, 260), (260, 180), (300, 100), (316, 12).